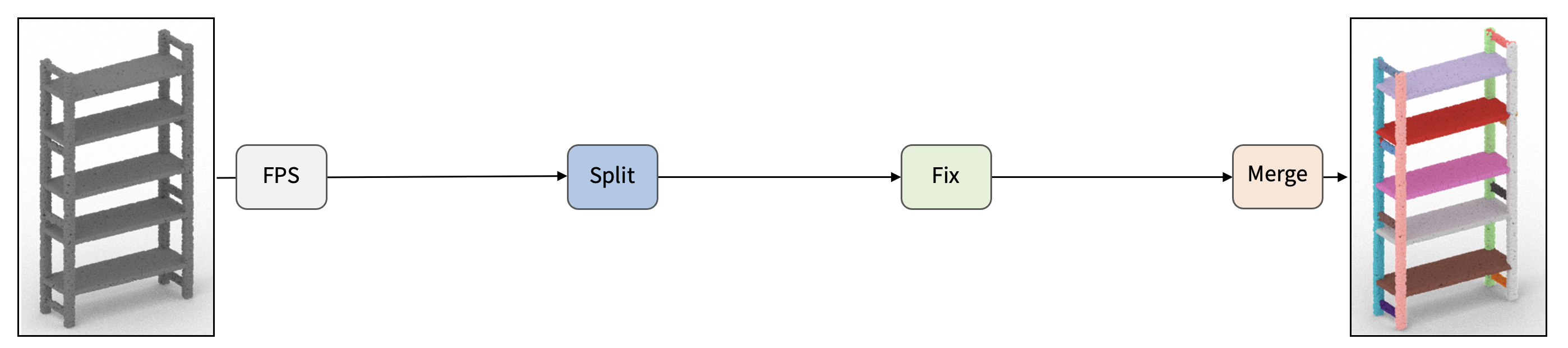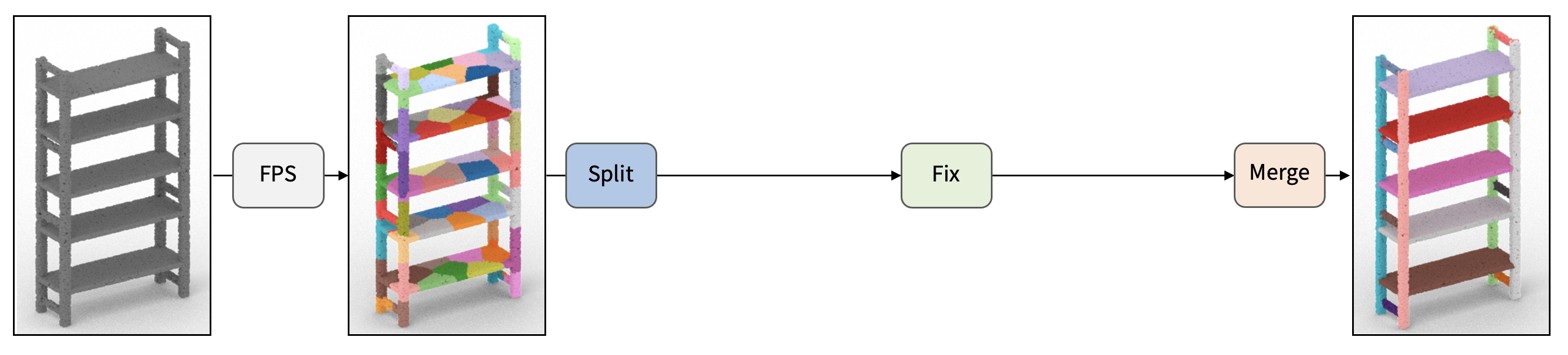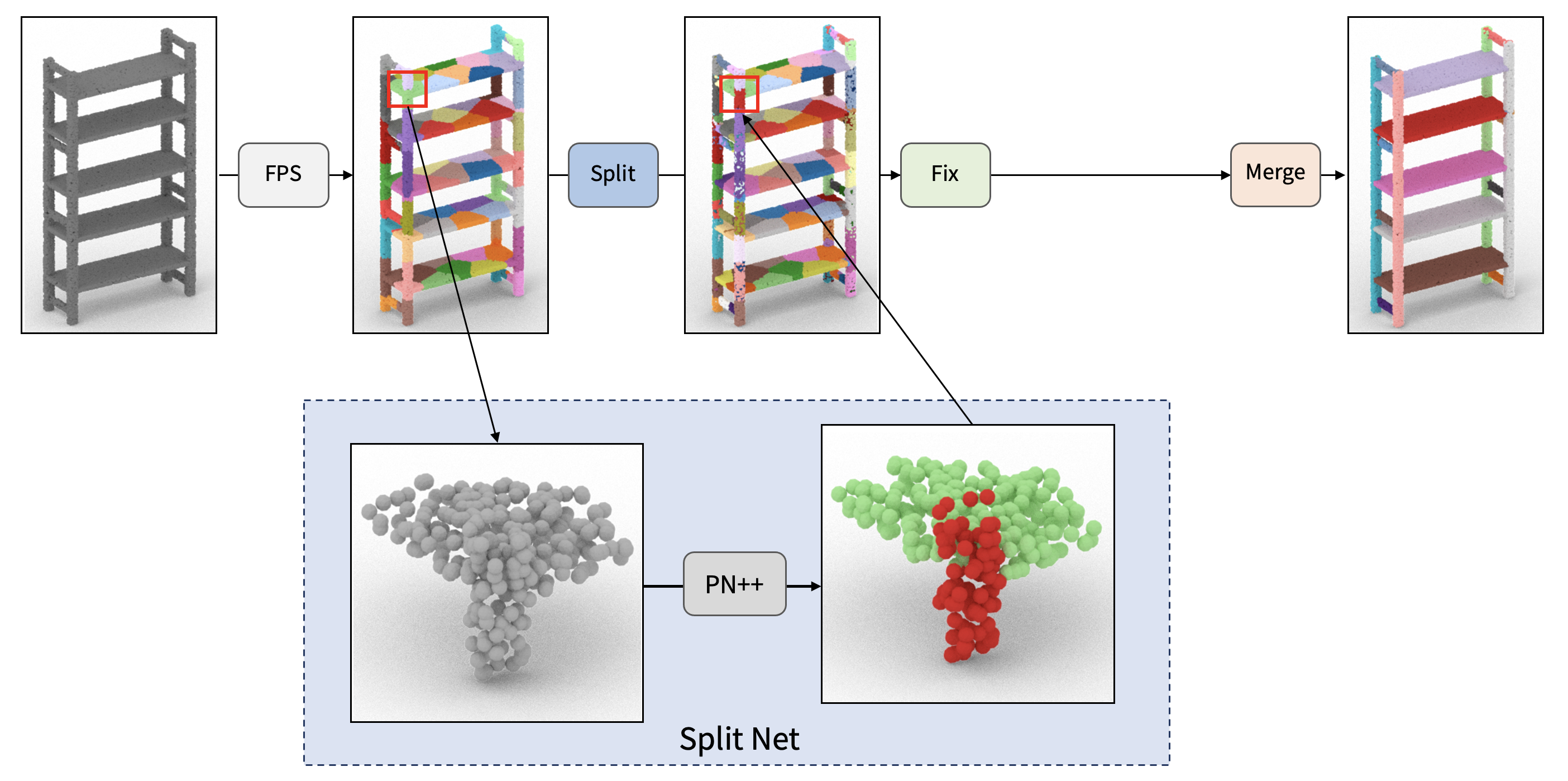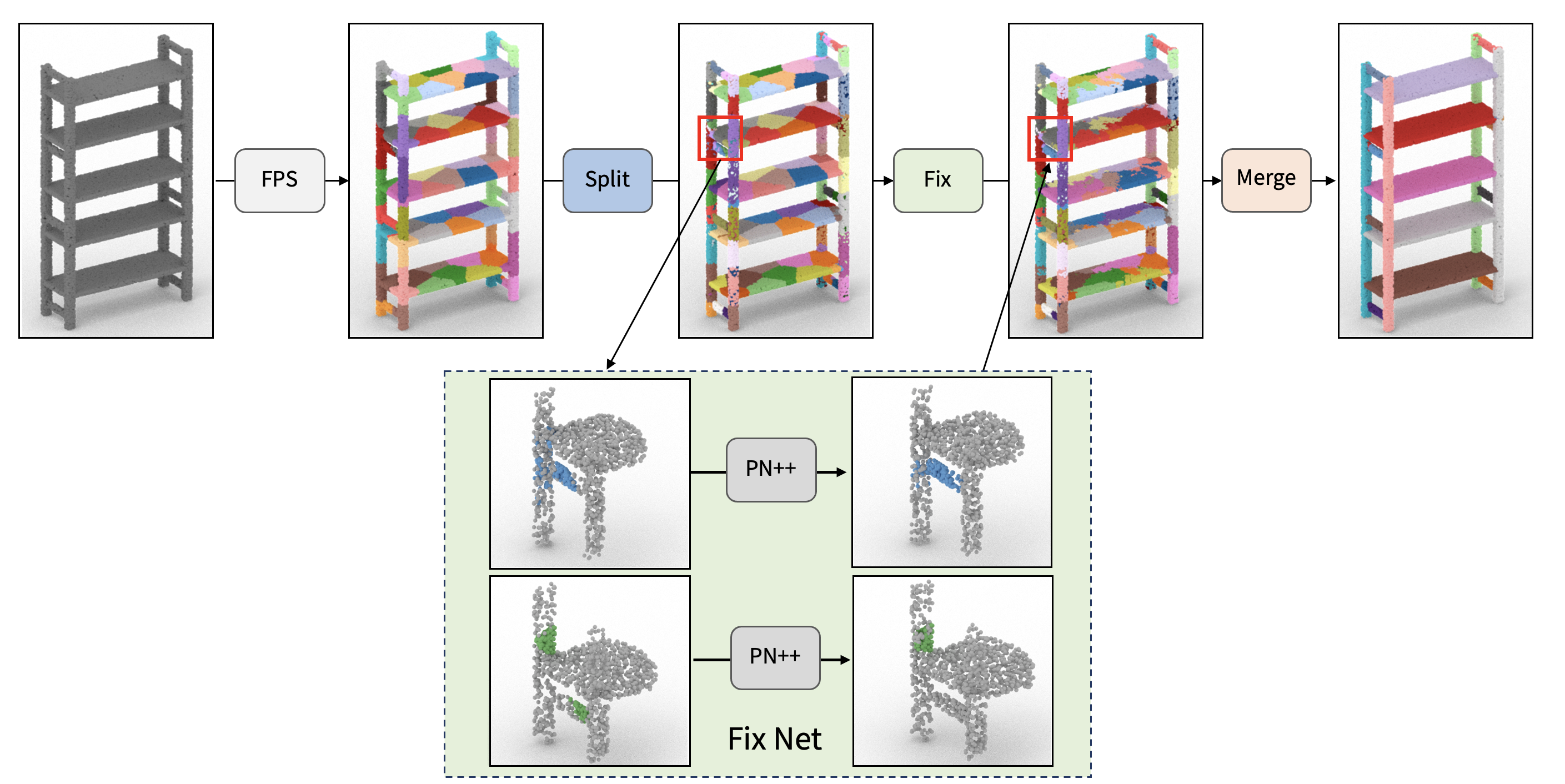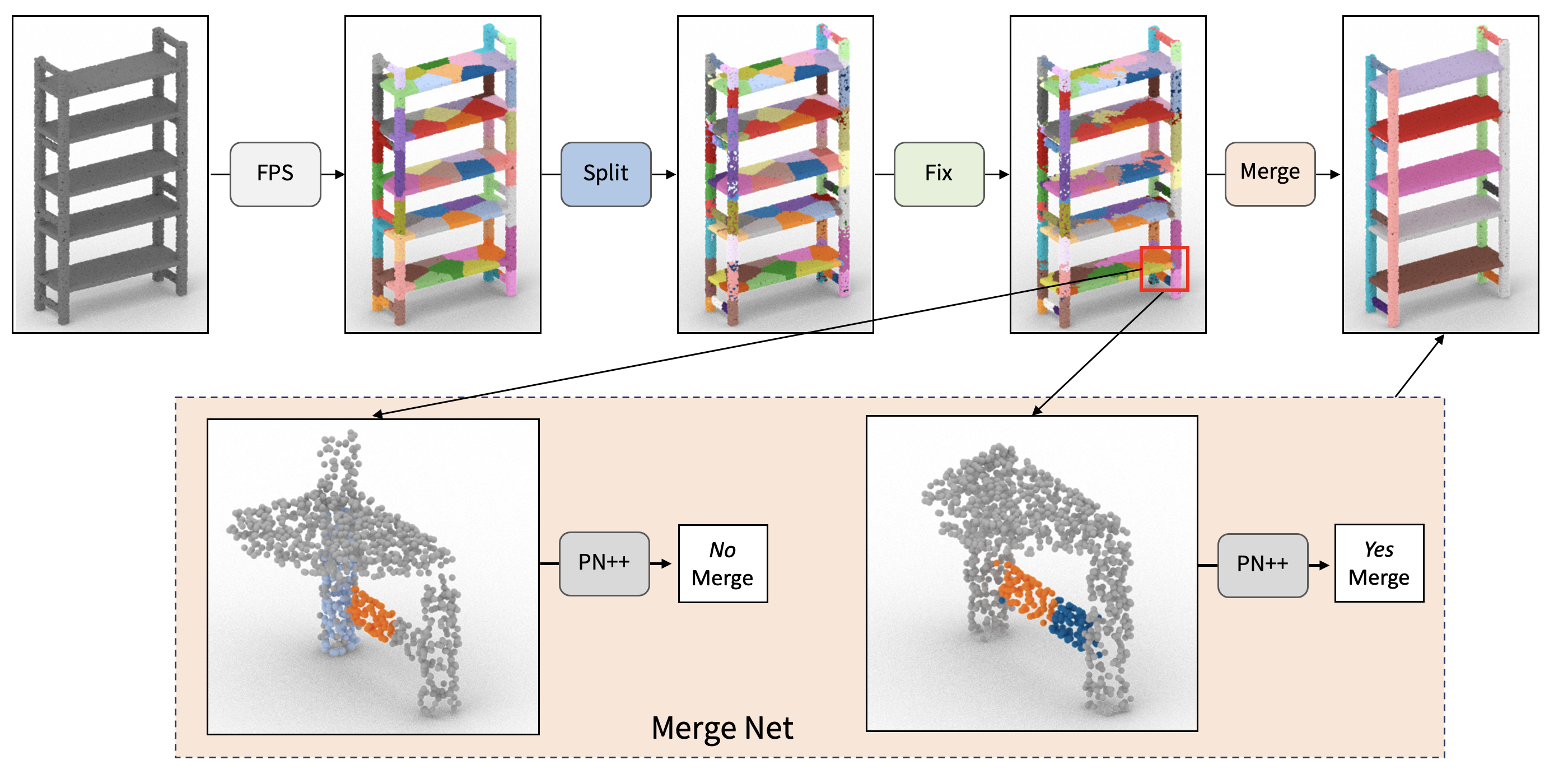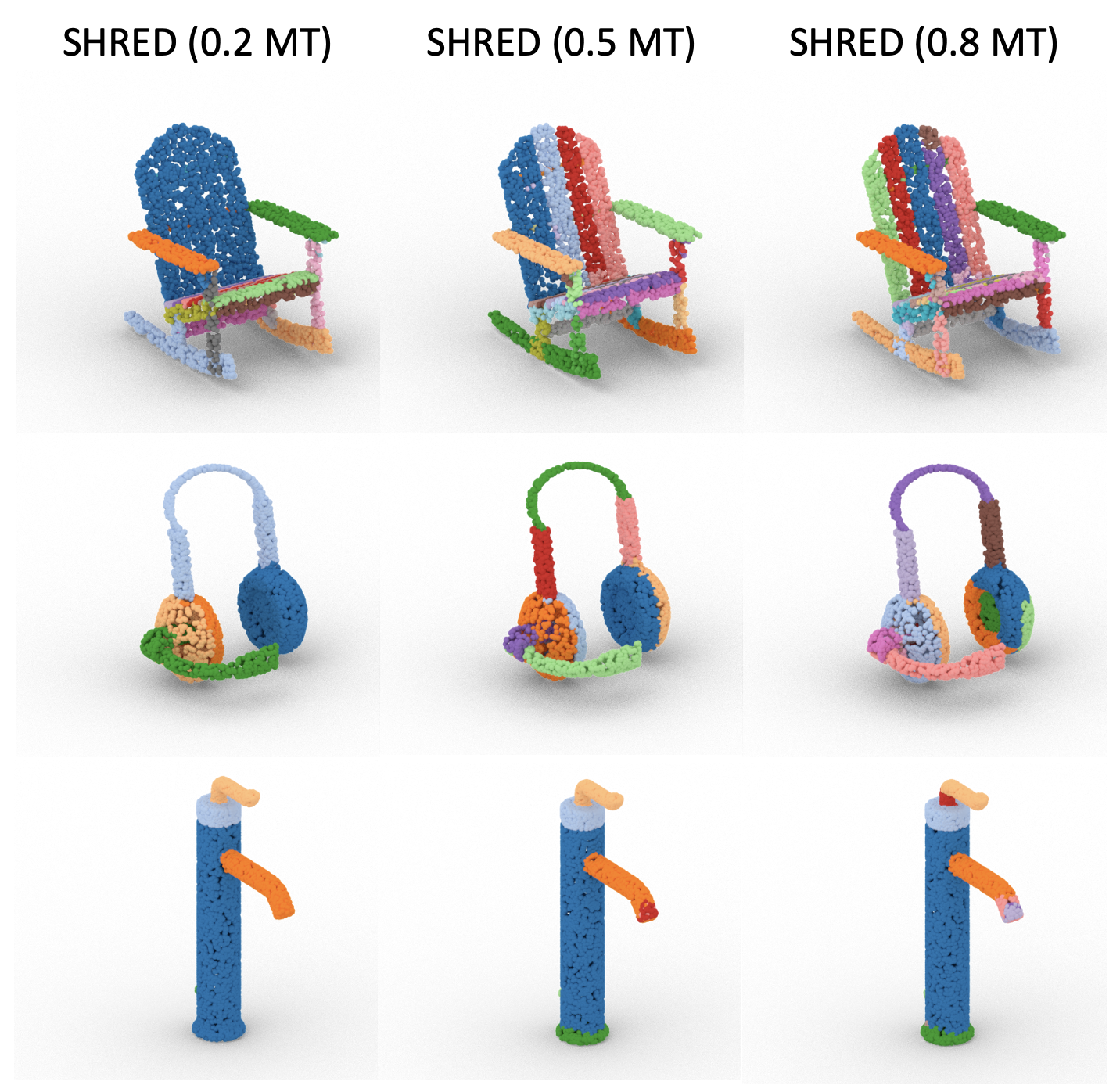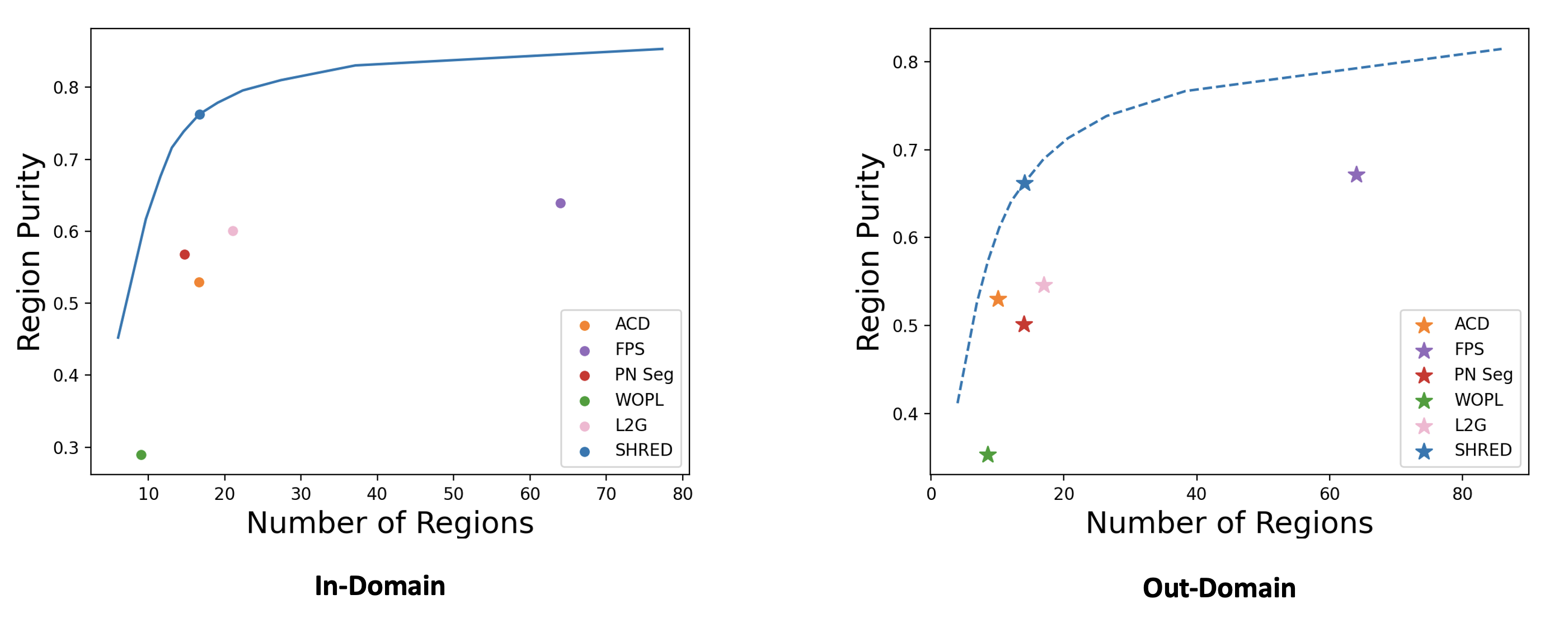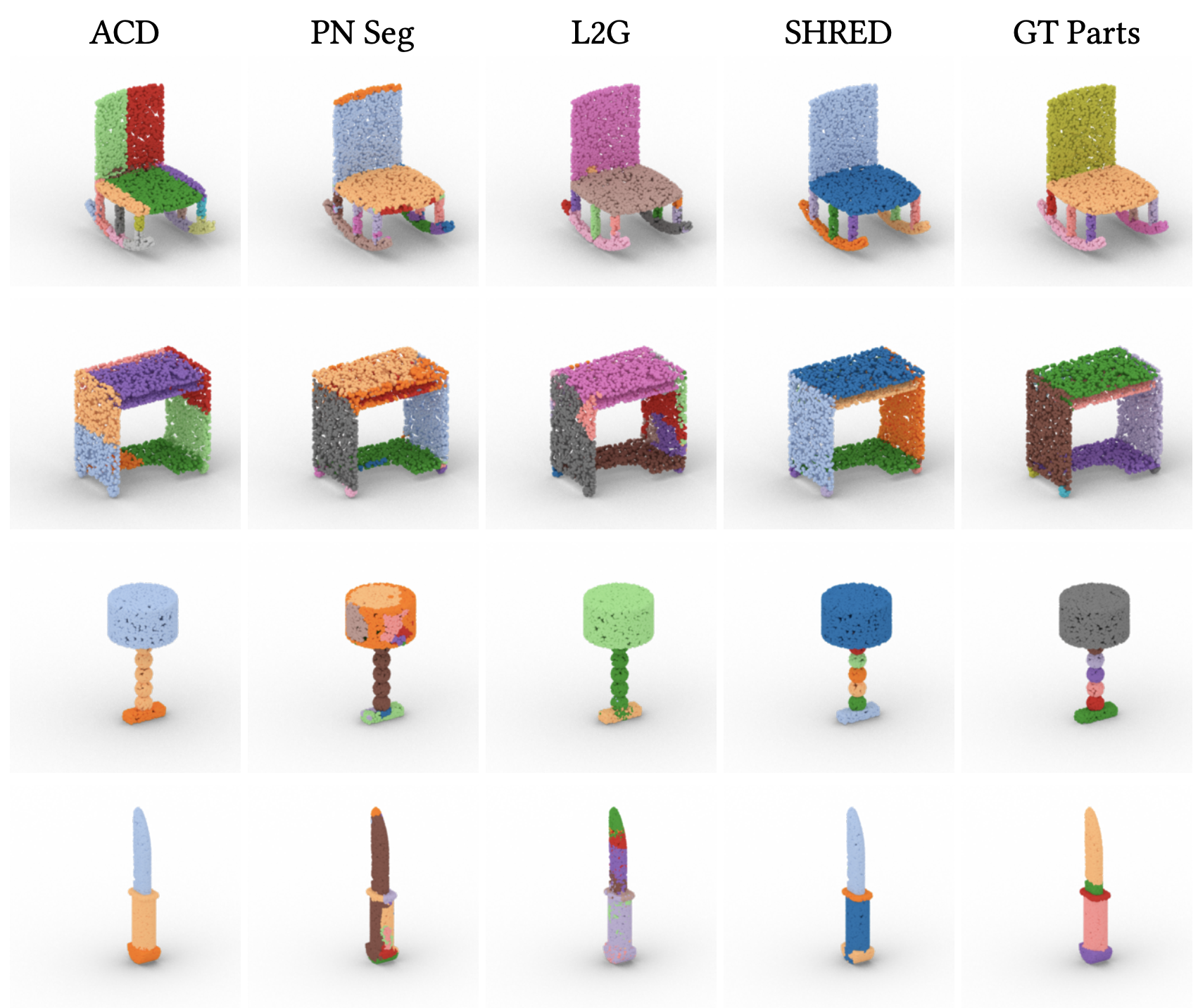
SHRED: 3D Shape Region Decomposition with Learned Local Operations

R. Kenny Jones Aalia Habib Daniel Ritchie

Brown University

Paper | Code | Video | Supplemental

SIGGRAPH Asia 2022

SHRED is a method for 3D SHape REgion Decomposition. It takes a 3D point cloud as input and uses learned local operations to produce a segmentation that approximates fine-grained part instances. A merge-threshold parameter can be adjusted to change decomposition granularity depending on the target downstream application.

Bibtex

@article{jones2022SHRED,
  title={SHRED: 3D Shape Region Decomposition with Learned Local Operations},
  author={Jones, R. Kenny and Habib, Aalia and Ritchie, Daniel},
  journal={ACM Transactions on Graphics (TOG)},
  volume={41},
  number={6},
  year={2022},
  publisher={ACM},
  address = {New York, NY, USA},
  articleno = {186}
}

Abstract

We present SHRED, a method for 3D SHape REgion Decomposition. SHRED takes a 3D point cloud as input and uses learned local operations to produce a segmentation that approximates fine-grained part instances. We endow SHRED with three decomposition operations: splitting regions, fixing the boundaries between regions, and merging regions together. Modules are trained independently and locally, allowing SHRED to generate high-quality segmentations for categories not seen during training.

We train and evaluate SHRED with fine-grained segmentations from PartNet; using its merge-threshold hyperparameter, we show that SHRED produces segmentations that better respect ground-truth annotations compared with baseline methods, at any desired decomposition granularity. Finally, we demonstrate that SHRED is useful for downstream applications, out-performing all baselines on zero-shot fine-grained part instance segmentation and few-shot fine-grained semantic segmentation when combined with methods that learn to label shape regions.

SHRED Method

SHRED takes a 3D shape as input and outputs a fine-grained region decomposition. We represent 3D shapes as high-resolution point-clouds sampled from a surface-mesh, as shown in the left. SHRED creates a segmentation by assigning a region to each input point, as shown in the right, where points in the same region share the same color. SHRED produces segmentations by running the input shape through 4 stages in a sequential fashion.

As SHRED’s learned operations all reason locally, the first step is to create a naive initial decomposition of the input shape. While there are many approaches that could be used here, we found that a simple Farthest Point sampling clustering procedure proved both fast and effective.

Split Operation

The split operation breaks regions into sub-regions. It consumes the regions output from the FPS stage, where each region might be an under-segmentation with respect to the ground-truth parts.

To remove this under-segmentation, the split operation uses a Split Network, that we model with a PointNet++. The split network consumes points from a single region as input, as show in grey on the left, and then makes an instance segmentation prediction for each input point, shown with the different colors on the right.

The split operation runs the split network on every input region, and then propagates these predictions back to global shape-view, in order to produce an over-segmented output decomposition.

Fix Operation

The fix operation is responsible for improving the boundaries between regions. It consumes the region decomposition output by the split operation. This decomposition is often fine-grained, but it might contain errors on region boundaries, as the split network receives no information about the shape outside of each region.

To accomplish this goal, the fix operation uses a fix network, that we model with a PointNet++. The fix-network operates over individual regions, shown in color on the left, but also receives nearby points from outside the region as input, show in grey on the left. The fix network is tasked with making a binary prediction for every input-point, of whether or not that point belongs to the region, which we represent with the colored versus grey points on the right.

The fix operation, once again, applies the fix network to every input region, and then propagates each local prediction back to the global shape-view, in order to produce a shape decomposition with better aligned boundaries.

Merge Operation

The merge operation decides when neighboring regions should be combined. It consumes the output of the fix module, so typically the input decomposition contains little under-segmentation, but uses many more regions than necessary.

The merge operation uses a merge network, modeled with a PointNet++. The merge-network operates on points sourced from two neighboring regions, represented with the different colors along with points from a local neighborhood that don’t belong to either region, represented with grey. This network makes a single binary prediction of whether or not the two regions should be merged together. We convert this prediction into a probability, and complete the merge if the prediction is above a merge-threshold hyper-parameter.

The merge operation runs the merge network iteratively over all pairs of neighboring regions, until all remaining pairs have been considered. This final set of regions is then considered as the output of the SHRED method, as show on the right in the top-row.

SHRED Results

We train SHRED on shapes from the PartNet dataset, with the finest-grained part annotations as the target segmentations.

SHRED trains on 3 in-domain categories: chairs, lamps, and storage furniture. We hold out 7 out-domain categories of shapes that we use to evaluate SHRED's generalization capabilities.

We show segmentations produced by SHRED with three merge-threshold settings. From left to right these are: 20%, 50% which is the default setting, and 80%.

When the merge-threshold is set below 50%, more regions will be merged together, and as the merge-threshold is increased the decomposition will be more fine-grained.

Given a GT annotation R*, we desire a region decomposition R that satisfies two properties: First, the number of regions in 𝑅 should not exceed the number of regions in 𝑅*, otherwise there will be over-segmentation. Second, each region of R should be a subset of some region in R*, otherwise there will be under-segmentation in R. These two properties work against one another, and are in fact only satisfied when R is exactly equal to R*, so we designed metrics that measure violations of these two properties.

We can easily measure violations of the first property by just counting the number of regions in the output segmentations, we call this measure decomposition granularity.

To measure violations of the second property, we use a metric we call region purity. This metric takes values from 0-1, and is equal to 1 only when all predicted regions are subsets of GT regions, but it’s values are not-sensitive to the granularity of the predicted decomposition.

We can consider the trade-off that different methods make in this decision space, by plotting granularity on the X-axis, and purity on the Y-axis. In this graph we want to be closest to the top-left corner, as this would make the best trade-off between region purity and the decomposition granularity. We show results for different 3D shape segmentation methods, with in-domain results on the left plot and out-domain results on the right plot. We compare SHRED, in blue, against a suite of comparison methods.

We vary the merge-threshold parameter to plot SHRED decomposition results as a frontier curve, and in all cases, we find that the SHRED frontier dominates the other methods, indicating it finds a strictly better trade-off between granularity and quality.

Fine-grained Part Instance Segmentation

Decompositions produced by SHRED can be treated as fine-grained part instance segmentations.

Top: We depict some qualitative outputs on test-set shapes, comparing segmentations produced by baseline methods in the left 3 columns, against the segmentations produced by SHRED, in the 4th column, where the GT annotation is shown in the rightmost column. As evidenced, even for shapes from out-domain categories, SHRED is able to produce high-quality segmentations.

Bottom: We evaluate different methods' ability to perform fine-grained part instance segmentation with an average IoU metric, that measures agreement between a predicted and GT segmentation. We find that SHRED significantly outperforms comparison approaches for both in-domain and out-domain averages.

Fine-grained Semantic Segmentation

Additionally, we examine how SHRED can be used to improve fine-grained semantic segmentation performance when access to labeled data is limited. We combine SHRED with a recent approach, NGSP, that learns how to semantically label part regions.

Top: We compare predictions made by SHRED with NGSP against a baseline version that does not label shape regions, and find that SHRED's region decompositions better match GT annotations, as they regularize the predicted semantic segmentations.

Bottom: Quantitatively, we find that when using 10 or 40 labeled exemplars, SHRED regions lead to semantic segmentations with higher mean IoU compared with alternative region decomposition approaches, or not using regions at all.

Effect of Training Data

Here we show results from our ablation experiments to answer the question of how training data effects the performance of SHRED. We depict the average IoU performance of SHRED and the best performing baseline method for both in-domain and out-domain categories with the first two bars.

We retrain versions of SHRED, on just one category of shape, these experiments are the chair only, lamp only, and storage only bars. As can be seen, training on a single category significantly hurts SHRED's performance.

However, if we retrain SHRED with the same three in-domain categories, but use only 10% of the data per-category, the performance remains strong. In fact, this version achieves better average IoU than the best-baseline method or any single-category trained version.

Related Publications

The Neurally-Guided Shape Parser: Grammar-based Labeling of 3D Shape Regions with Approximate Inference
R. Kenny Jones, Aalia Habib, Rana Hanocka, Daniel Ritchie
CVPR 2022 Paper | Project Page | Code

Acknowledgements

We would like to thank the anonymous reviewers for their helpful suggestions. This work was funded in parts by NSF award #1941808 and a Brown University Presidential Fellowship. Daniel Ritchie is an advisor to Geopipe and owns equity in the company. Geopipe is a start-up that is developing 3D technology to build immersive virtual copies of the real world with applications in various fields, including games and architecture.