ShapeCoder:
Discovering Abstractions for Visual Programs
from Unstructured Primitives

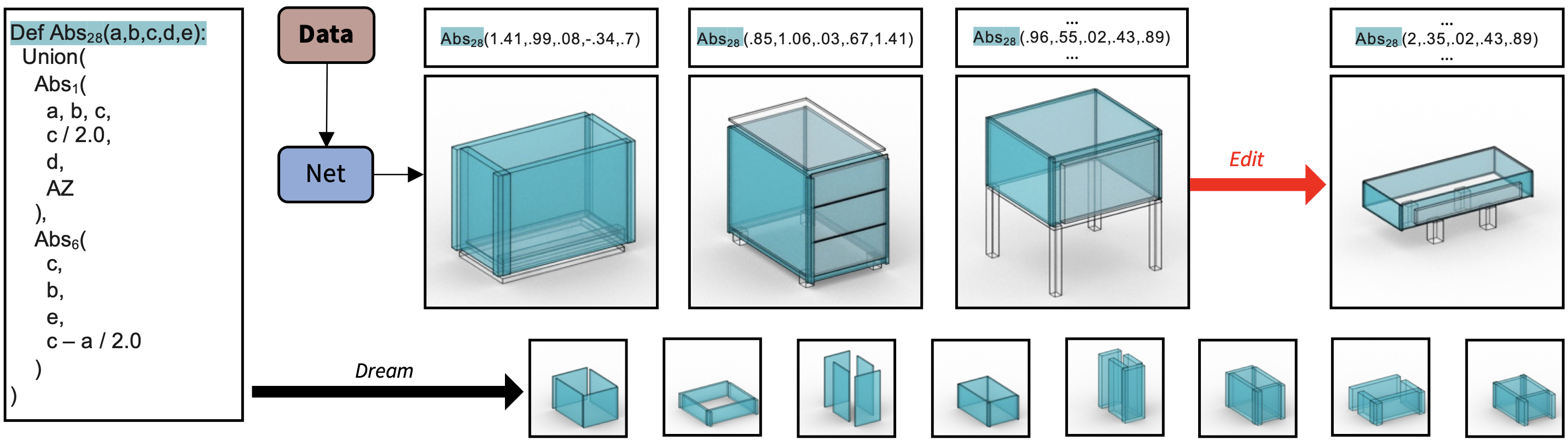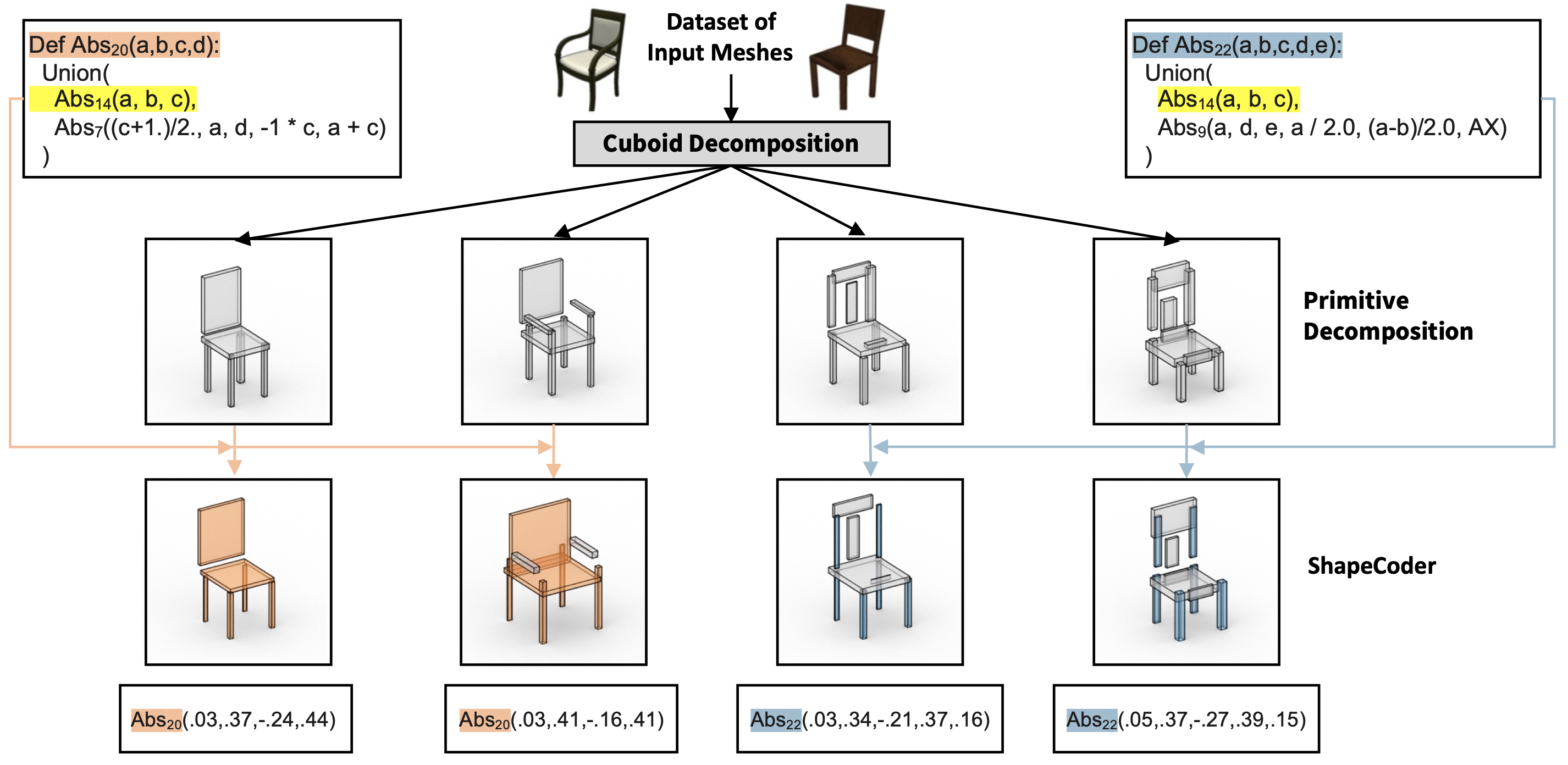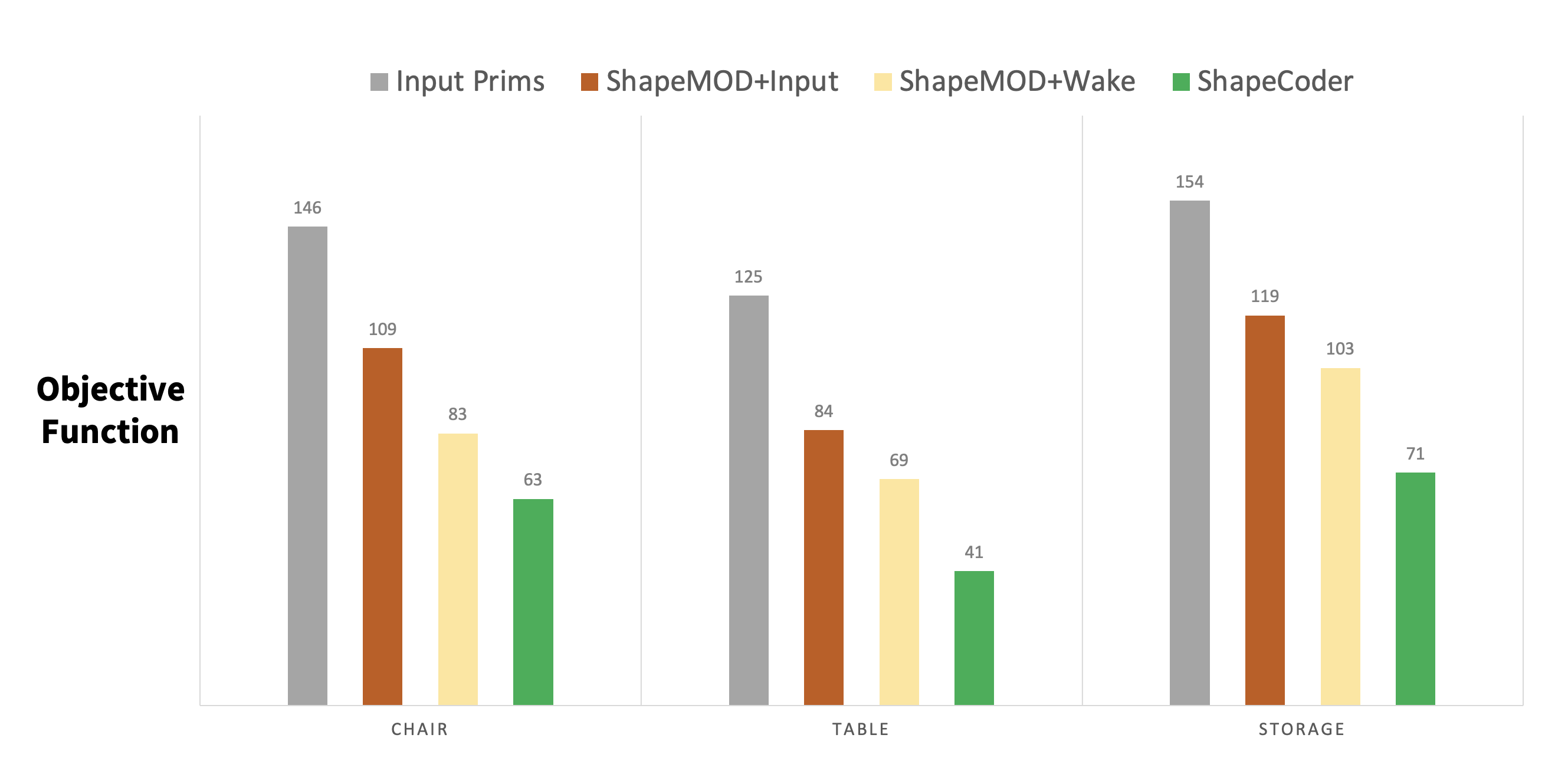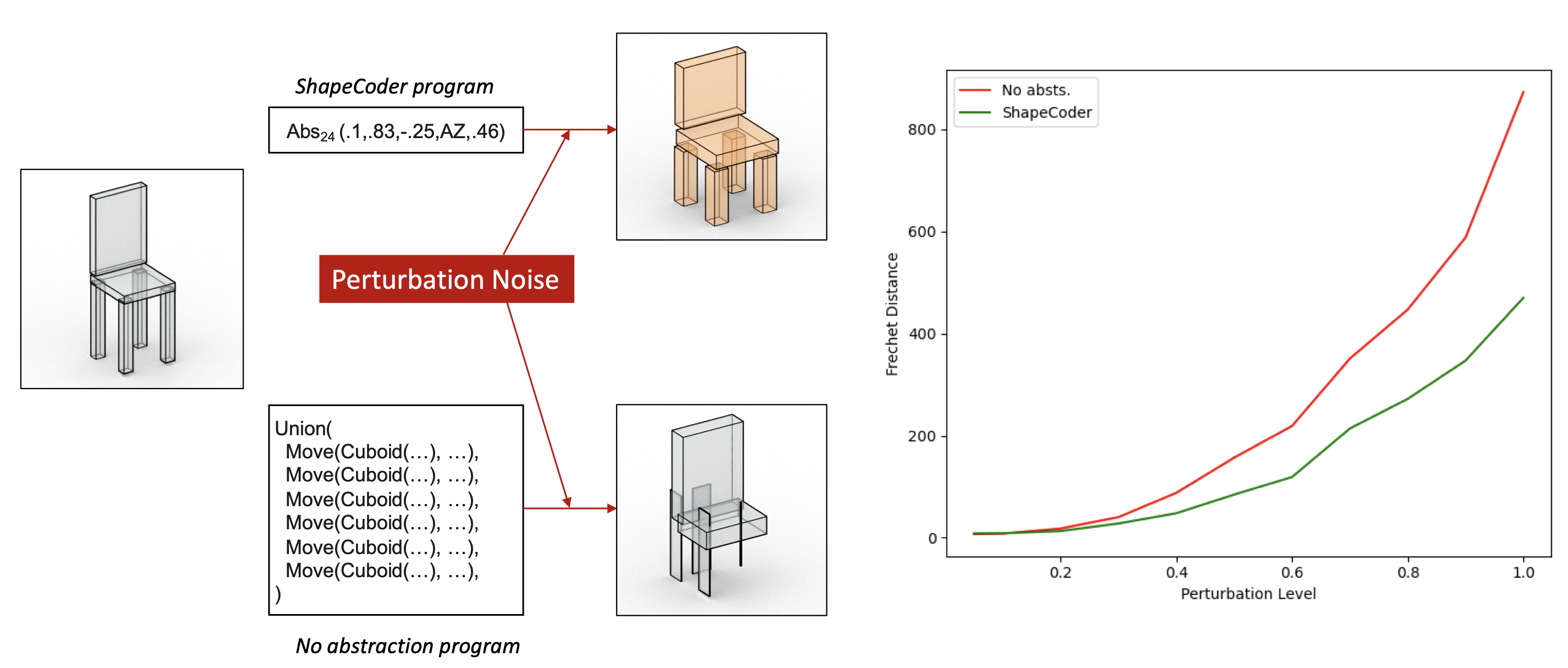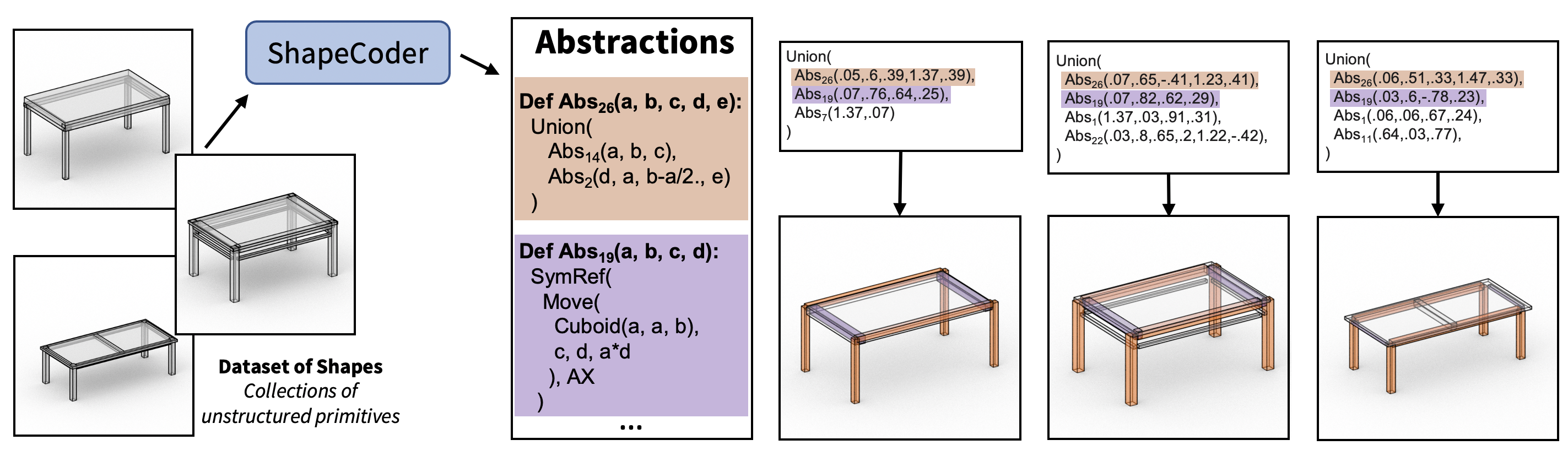
R. Kenny Jones1      Paul Guerrero2      Niloy J. Mitra2,3      Daniel Ritchie1     
1Brown University      2Adobe Research      3University College London     

Paper | Code | Supplemental

SIGGRAPH 2023




ShapeCoder automatically discovers abstraction functions, and infers visual programs that use these abstractions, to compactly explain an input dataset of shapes represented with unstructured primitives. For example, the orange abstraction uses only five parameters to encode a distribution of 4-legged table bases with adjoining horizontal support bars.


                       


Above, we show an input shape (left) and its corresponding primitive decomposition (right). Below we show parametric edits to the inferred ShapeCoder program (right), and how those edits can be transferred back to the original mesh (left).

                       



Bibtex 

@article{jones2023ShapeCoder,
  author = {Jones, R. Kenny and Guerrero, Paul and Mitra, Niloy J. and Ritchie, Daniel},
  title = {ShapeCoder: Discovering Abstractions for Visual Programs from Unstructured Primitives},
  year = {2023},
  issue_date = {August 2023},
  address = {New York, NY, USA},
  volume = {42},
  number = {4},
  journal={ACM Transactions on Graphics (TOG), Siggraph 2023},
  articleno = {49},
}

Abstract


We introduce ShapeCoder, the first system capable of taking a dataset of shapes, represented with unstructured primitives, and jointly discovering (i) useful abstraction functions and (ii) programs that use these abstractions to explain the input shapes. The discovered abstractions capture common patterns (both structural and parametric) across a dataset, so that programs rewritten with these abstractions are more compact, and suppress spurious degrees of freedom. ShapeCoder improves upon previous abstraction discovery methods, finding better abstractions, for more complex inputs, under less stringent input assumptions. This is principally made possible by two methodological advancements: (a) a shape-to-program recognition network that learns to solve sub-problems and (b) the use of e-graphs, augmented with a conditional rewrite scheme, to determine when abstractions with complex parametric expressions can be applied, in a tractable manner. We evaluate ShapeCoder on multiple datasets of 3D shapes, where primitive decompositions are either parsed from manual annotations or produced by an unsupervised cuboid abstraction method. In all domains, ShapeCoder discovers a library of abstractions that captures high-level relationships, removes extraneous degrees of freedom, and achieves better dataset compression compared with alternative approaches. Finally, we investigate how programs rewritten to use discovered abstractions prove useful for downstream tasks.



ShapeCoder Method Overview




ShapeCoder aims to discover a library of abstractions, and programs that use those abstractions, to represent shapes in the input dataset. It determines which abstractions should be added into the library according to an objective function, which trades off two terms: program complexity, measured by degrees of freedom in the discovered programs, and library complexity, measured by the number of added abstractions into the library. These two terms regularize one another, as finding more compact programs requires adding abstractions into the library. ShapeCoder's goal is to find a tractable set of such abstractions that captures and constrain the common patterns in the input dataset.


This is a hard objective to optimize directly, so we break this task into multuple steps that each tackle a tractable sub-problem. A dream phase trains a recognition network, that converts collections of primitives into programs, by sampling synthetic data from the library. A wake phase uses the recognition network to infer programs that explain the input shapes in the dataset. A proposal phase reasons over shapes inferred from wake, and generates a set of candidate abstraction functions. An integration phase consumes the candidate abstraction functions, and determines which of them should be added into the library in order to best optimize the objective function. Central to the the integration phase is a refactor operation that uses e-graphs, a data structure from the programming languages community, to find minimal cost equivalent programs under a specific library version.




Running ShapeCoder on primitive decomposed shapes


We give ShapeCoder access to a base DSL with low-level 3D shape modeling functions, and run it over collections of primitive-decomposed shapes sourced from PartNet annotations, removing all semantic and hierarchical information. We find that across different input shape categories, ShapeCoder is able to consistently discover compelling high-level abstractions applicable to the input shape collections. These abstractions capture diverse geometric expressions, while constraining many extraneous degrees of freedom through parametric and structural relationships. Below we show some examples of discovered abstractions applied within inferred programs. We additionally show how parametric edits of those programs support shape manipulation, and visualize some representative dreams from each function, to give an idea of what kinds of geometry each function is capable of representing.



Abstractions in later rounds of ShapeCoder can reference previously discovered abstractions in sub-function calls, forming a nesting hierarchy of abstractions. For instance, when run on chairs, ShapeCoder discovers a top-level abstraction that explains a common layout of a complete chair, with only five free parameters.





These abstractions can even be helpful for structural analysis of 3D shapes. For instance, the below discovered abstraction for tables consistently maps to the outermost legs in a table base, even though that part grouping has a wide-range of possible output geometries.





When run over storage furniture, ShapeCoder discovers the following abstraction that corresponds with common pattern of creating the four upright sides of a drawer component.





Discovering abstractions over unsupervised primitive decompositions





Beyond clean primitive decompositions, Shapecoder can also well-handle inputs that are noisy and less regular. Starting with meshes from ShapeNet, we emply a pretrained unsupervised primitive decomposition method to form an input dataset of shapes. When we run ShapeCoder on this input, we observe that it is still able to discover high-level abstractions that have reasonable semantic interpretations and can be broadly applied across the shape collection.



ShapeCoder improves compression-based objective



ShapeCoder is guided by its compression-based objective function, but how well can it optimize it? We compare the starting objective value from the input primitives (grey bar) to the objective value found by ShapeCoder (green bar), and observe that ShapeCoder is able to make a significant improvement. We compare ShapeCoder to two alternative approaches, running ShapeMOD over naive programs parsed from input primitives (red bar) or over programs inferred from ShapeCoder's wake phase (yellow bar), and find that ShapeCoder best optimizes our objective.



Abstractions semantically constrain program output



We would like our discovered abstractions to help semantically constrain output executions, for instance compare a naive program sourced from input primitives (left, bottom) against a program rewritten with ShapeCoder abstractions (left, top). To evaluate whether the discovered abstractions are successful in removing extraneous degrees of freedom, we can add artificial perturbations to the parameters of these two types of programs and observe how the output geometry changes. We run an experiment (right), where various levels of perturbation noise are added to a large collection of shape programs, and we track how well the executed outputs ‘stay in distribution’ by measuring frechet distance against a validation set. From this experiment, we observe that rewriting programs with our discovered abstractions helps to semantically constrain their output.




Related Publications

ShapeMOD: Macro Operation Discovery for 3D Shape Programs
R. Kenny Jones, David Charatan, Paul Guerrero, Niloy J. Mitra, and Daniel Ritchie
SIGGRAPH 2021 Paper | Project Page | Code

DreamCoder: bootstrapping inductive program synthesis with wake-sleep library learning
Kevin Ellis, Catherine Wong, Maxwell Nye, Mathias Sablé-Meyer, Lucas Morales, Luke Hewitt, Luc Cary, Armando Solar-Lezama, and Joshua Tenenbaum
PLDI 2021 Paper

Neurosymbolic Models for Computer Graphics
Daniel Ritchie, Paul Guerrero, R. Kenny Jones, Niloy J. Mitra, Adriana Schulz, Karl D. D. Willis, and Jiajun Wu
Eurographics 2023 STAR Paper

egg: Fast and extensible equality saturation
Max Willsey, Chandrakana Nandi, Yisu Remy Wang, Oliver Flatt, Zachary Tatlock, and Pavel Panchekha
POPL 2021 Paper | Project Page

Unsupervised learning for cuboid shape abstraction via joint segmentation from point clouds
Kaizhi Yang and Xuejin Chen
SIGGRAPH 2021 Paper | Code

ShapeAssembly: Learning to Generate Programs for 3D Shape Structure Synthesis
R. Kenny Jones, Theresa Barton, Xianghao Xu, Kai Wang, Ellen Jiang, Paul Guerrero, Niloy J. Mitra, and Daniel Ritchie
SIGGRAPH Asia 2020 Paper | Project Page | Code

Acknowledgements

We would like to thank Srinath Sridhar and the anonymous reviewers for their helpful suggestions. Renderings of shape programs were produced using the Blender Cycles renderer. This work was funded in parts by NSF award #1941808, a Brown University Presidential Fellowship, and an ERC grant (SmartGeometry). Daniel Ritchie is an advisor to Geopipe and owns equity in the company. Geopipe is a start-up that is developing 3D technology to build immersive virtual copies of the real world with applications in various fields, including games and architecture.